Lasso

속성의 숫자가 레코드보다 더 많은 경우 발생할 수 있는 문제는 오버피팅(overfitting)이다. 이는 레코드에서 sparse하게 나타난 패턴을 적절하지 않은 속성으로 과대 해석하게 됨으로써 발생하게 된다. 이 때문에 속성 선택 과정을 거치거나 혹은 더 많은 데이터를 구하는 과정을 거치게 된다.

위와 같은 경우는 앞으로 IoT(Internet of Things)가 일반화되어 특정 단위 시간에 다양한 종류의 데이터가 쏟아지게 되면서 더 큰 이슈로 부상할 것이며, 이미 바이오정보학에서는 일반화된 문제이다.

최근 이런 이슈때문에 주목을 받고 있는 방법론이 Lasso (least absolute shrinkage and selection operator)이다.

Lasso는 모형의 Bias를 다소 올리면서 Variance error를 줄이는 방식을 취하는데, 이때문에 모형이 다소 복잡해지는 측면이 있으나 Variance 에러가 획기적으로 줄기 때문에 전체 에러를 줄이게 되는 효과를 발휘해 실무에서 많이 활용되고 있다.

위 식에서 $\lambda$는 추정해야 될 부분으로 대부분의 경우 cross-validation으로 최적값을 찾게 된다. $\lambda$가 0이면 일반적인 최소제곱법을 제공하게 되고 \(\lambda\) 충분히 크다면 모든 추정치가 0인 intercept만 존재하는 모형이 만들어진다.

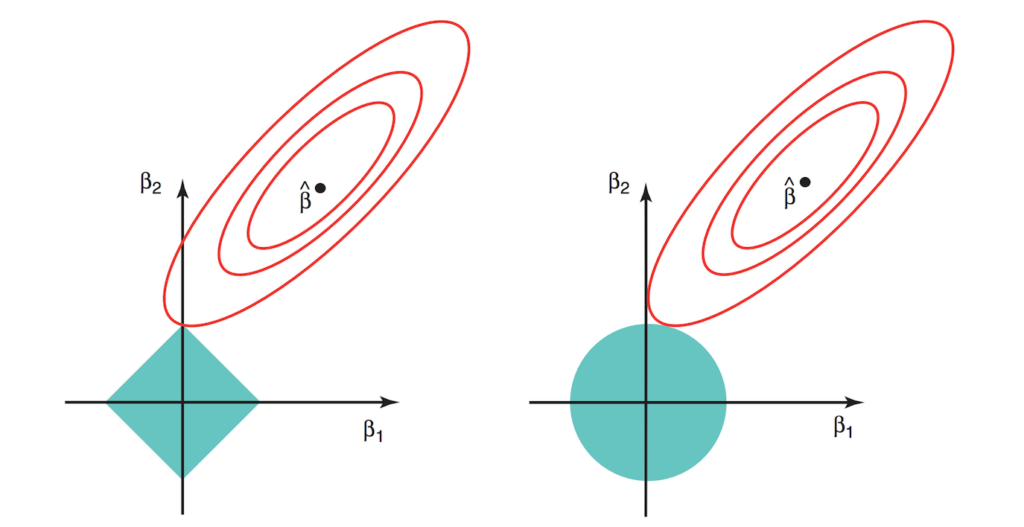
위 그림은 Lasso를 설명하는 가장 유명한 그림으로 왼쪽이 Lasso, 오른쪽이 Ridge 방법을 의미한다. 등고선은 RSS가 일정한 부분을 의미하고 푸른 영역은 $\lambda$가 포함된 constraint function을 의미한다. Ridge와 Lasso의 가장 큰 차이점은 $l_1$norm이냐 $l_2$norm이냐의 차이인데, $l_1$일 경우 manhattan distance와 형태의 함수를 제공하고, $l_2$일 경우 euclidean distance 형태의 함수를 제공하는 차이를 보여주는데, 이 부분이 그래프에 표현 되어 있다. Lasso의 경우 최적값은 모서리 부분에서 나타날 확률이 Ridge에 비해 높아 몇몇 유의미하지 않은 변수들에 대해 계수를 0에 가깝게 추정해 주어 변수 선택 효과를 가져오게 된다. 반면 Ridge의 경우 어느정도 상관성을 가지는 변수들에 대해서 pulling이 되는 효과를 보여줘 변수 선택보다는 상관성이 있는 변수들에 대해서 적절한 가중치 배분을 하게 된다. 따라서 Ridge의 경우 PCA와 상당한 관련성이 있다.

필자의 경우 Lasso는 stepwise elimination의 훌륭한 대안으로 활용하고 있다. 실제 stepwise elimination은 이 방법을 구동할때마다 다른 변수 선택이 이루어져 일관성을 보여주지 못한다. 하지만 Lasso의 경우 모델 메트릭스가 general position일 경우 항상 동일한 값을 보여준다는 것이 증명되어 있다. 게다가 느린 stepwise elimination에 비해 상당히 빠르다.

고차원 문제와 오버피팅

위 Lasso와 Ridge 모두 변수가 많은 경우 모델 오버피팅을 피하기 위한 방법중에 하나이며, 이곳에 존재하는 \(l_1\), \(l_2\) norm의 경우 딥러닝에서 오버피팅을 방지하기 위한 용도로까지 활용되고 있다. 하지만 방법론 자체가 오버피팅을 완전히 피할 수 있게 하지는 않는다. 필자가 지금까지 모델링을 결과를 보면서 가장 애를 먹은 부분은 오버피팅문제이고, 지금도 이 이슈는 나를 가장 곤혹스럽게 한다. 단순히 학습셋에서 테스트셋을 쪼개 검증하는 과정을 반복하면서 MSE가 0에 가깝게 나왔다고 엄청난 성능 개선을 했다고 좋아하다가 나중에 실제 미래 데이터에서 성능이 엉뚱하게 나오는 경우에 오버피팅이 발생한 걸 뒤늦게 발견하고 후회해본 경험이 있다면 필자의 마음을 이해할 수 있을 것이다. 참고로 10개의 속성으로 단 두개의 학습셋에 피팅을 해서 MSE 0이 도출되는건 매우 쉽다. 그러나 그렇게 나온걸 여러분이 목적으로 삼은 모형이라 할 수 있는가? 더 많은 데이터 혹은 내일 생성될 데이터를 입력할때 동일한 성능을 보여줄 것으로 생각할 수 있을 것인가?

이런 오버피팅을 피할 수 있는 가장 좋은 방법은 적절한 검증셋을 구축하는 것이다.
많은 분들이 검증셋과 테스트셋을 구분하지 못하는데, 검증셋은 모형이 구축될 당시의 어떠한 관련 정보가 포함되어 있지 않은 셋으로 구성된 셋을 의미한다. 필자의 경우 모형에 쓰일 변수를 선택하는데 Information Value(IV)값을 주로 참고하고, 실제 날짜 정보(예를 들어 년월)를 모형에 넣지는 않지만 날짜정보도 함께 IV값으로 확인한다. 만일 날짜 정보의 IV가 높다면 검증셋은 반드시 out-of-time 데이터로 구축해야 된다고 판단한다(초심자들은 날짜를 변수로 그대로 넣어 성능향상을 했다고 이야기하기도 하는데, 이럴 경우 spurious regression 문제가 발생한다. 날짜를 바로 넣기 보다는 그러한 효과를 일으킨 원인 변수를 찾는 작업을 통해 해당 원인 변수를 적용해야 된다). 결과적으로 트레이닝에 쓰인 데이터의 날짜와 겹치지 않는 미래 혹은 과거의 데이터로 모형을 다시한번 검증해야 된다는 것이다.
이 이외에 validation set을 구축하는 방법은 속칭 golden set을 구축하면서 수행된다. 모형의 성능을 객관적으로 평가할 수 있는 셋을 추가로 구축하는데, 대부분 사람이 구성하게 된다. 요망하는 모형의 decision boundary를 가이드 하는 흡사 SVM의 support vector와 같은 데이터들로 별도 셋을 구성해 놓는 것이라고 생각하면 된다.

일단 구축이 되면 test set 퍼포먼스와 validation set 퍼포먼스를 맞추기 위해서 다양한 시도를 하게 되는데, 이 부분이 모델링의 백미이며, 이 과정을 통해 실제 test와 validation set 모두의 퍼포먼스 향상을 가져오기도 하고, 모형이 더 간단해지면서 해석이 쉬워지기도 한다.

최근에 다양한 분석 모델링 도구들이 나오고 많은 책들이 소개되고 있는 가운데 개인적으로 가장 아쉬운 부분은 무분별한 모델링으로 인해 간과하고 넘어가는 부분들이 상당히 많아지고 있다는 것이다. 이러한 부분들은 모델링 목적에 대한 완벽한 이해와 데이터에 대한 충분한 탐색을 함으로써 얻어지게 되는데 데이터만 주어지면 무작정 모델링을 하게 됨으로써 큰 낭패를 보는 경우가 허다하고 대부분의 경우 적절한 검증셋 준비가 없거나 테스트셋과 다를바 없는 검증셋으로 눈가리고 아웅식으로 진행하기 때문이다. 게다가 이럴 경우 의도치 않은 거짓말(?)을 하게 되기도 한다. 이렇게 된 이유중에는 빅 데이터가 활성화 되면서 일어난 데이터 다다익선(多多益善)미신이 한 몫 했다고 생각한다. 데이터는 뭐든지 추가하면 좋아질 것이라는 믿음은 오히려 데이터가 부족해서 과거에 많이 일어났던 오버피팅 문제를 속성이 많이 늘어나면서 생기는 오버피팅 문제로 전환을 시켜버렸다고 생각한다. 그리고 이러한 문제는 위와 같은 미신때문에 더 해소하기가 어려워졌다.

다시 말하자면 학습모델링 역시 더이상 뺄것이 없을 때 완벽해 진다는 것을 꼭 인지해야 될 것이다. 또한 검증셋은 반드시 모형의 목적에 맞는 그러한 데이터셋으로 엄격하게 구축해 나침반으로 사용해야 된다. 그러한 상황에서 Lasso 방법론도 올바른 모형을 건내줄 것이다.

참고문헌

• An introduction to statistical learning with R  : http://www-bcf.usc.edu/~gareth/ISL/

Lasso 그리고 고차원 문제와 오버피팅 by from __future__ import dream is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.